A binary tree is defined as a data structure that is non-linear in nature and follows a hierarchical structure. Also, it has a maximum of two children nodes for each of its parent nodes. The word binary is self-explanatory since it is associated with the number two.
Every node in a binary tree is associated with three distinct fields, namely:
- Data element
- Reference to the left child node
- Reference to the right child node
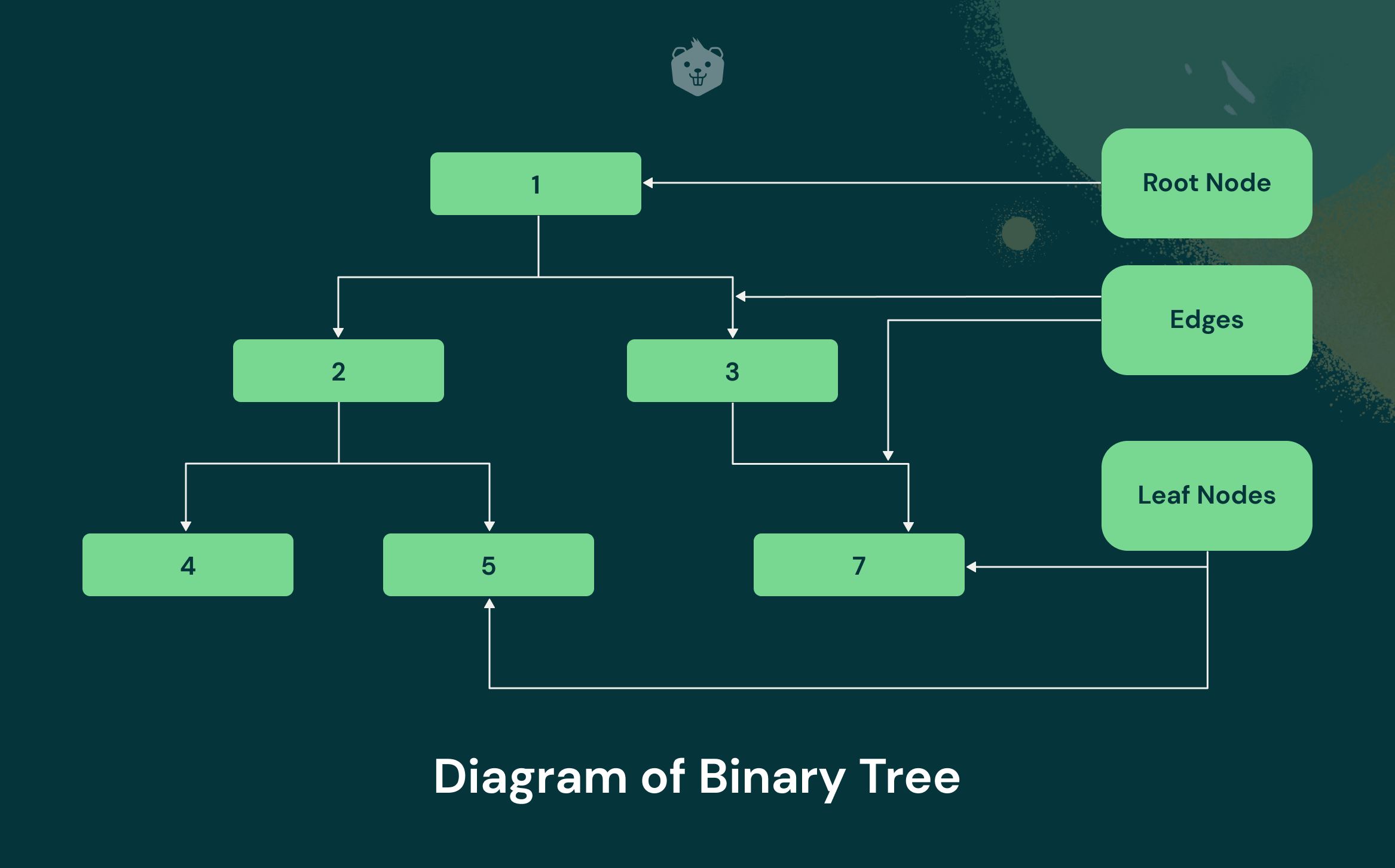
Given above is a simple diagram of a binary tree data structure. As you can see, the tree has a hierarchical structure and descends from a root node (with value 1). You may have also noticed that each of the nodes has at most 2 children nodes except for the leaf nodes. This is what categorizes this tree as a binary tree.
Basic Tree Terminology

Root Node
The initial node in a tree data structure is known as the Root Node. A root node is required for every tree. The root node is the starting point for the tree data structure. There can only be one root node in any tree. A tree can never have more than one root node.
Edge
The EDGE is the connecting line between any two nodes in a tree data structure. There will be a maximum limit of 'N-1' number of edges in a tree with 'N' nodes.
Parent Node
In a tree data structure, the predecessor node of any given node is called a parent node. In simpler terms, any node which has one or more children nodes associated with it is termed a parent node.
Child Node
In a tree data structure, the successor node of any given node is called a child node. In simpler terms, the descendant node of a given parent node is termed a child node.
Leaf Node
In a tree data structure, a terminating node without any subsequent children nodes is called a leaf node.
Internal Node
In a tree data structure, any node with one or more children nodes associated with it is called an internal node.
Degree
The total number of children nodes associated with a given node in a tree is called a degree.
Level
In a tree data structure, each step from the top to the bottom constitutes a level. For example, the root node is at level 0, the children of the root node are at level 1, and so on.
Height
The total number of edges in the longest path from a leaf node to any given node in a tree data structure is defined as the height of the given node.
The height associated with the root node is also the height of the tree data structure.
Properties of Binary Tree Data Structure

- The maximum number of nodes at each level ‘i’ of a binary tree is given by 2^i
- The minimum number of nodes at height ‘h’ of a binary tree is given by (h+1)
- The maximum number of nodes at height ‘h’ of a binary tree is given by (2^(h+1))-1
Various Types of Binary Tree Data Structure
Proper Binary Tree
It is a type of binary tree that has either two children or zero children for each node. It is also called a strict binary tree. Given below is a simple diagram to illustrate a proper binary tree.
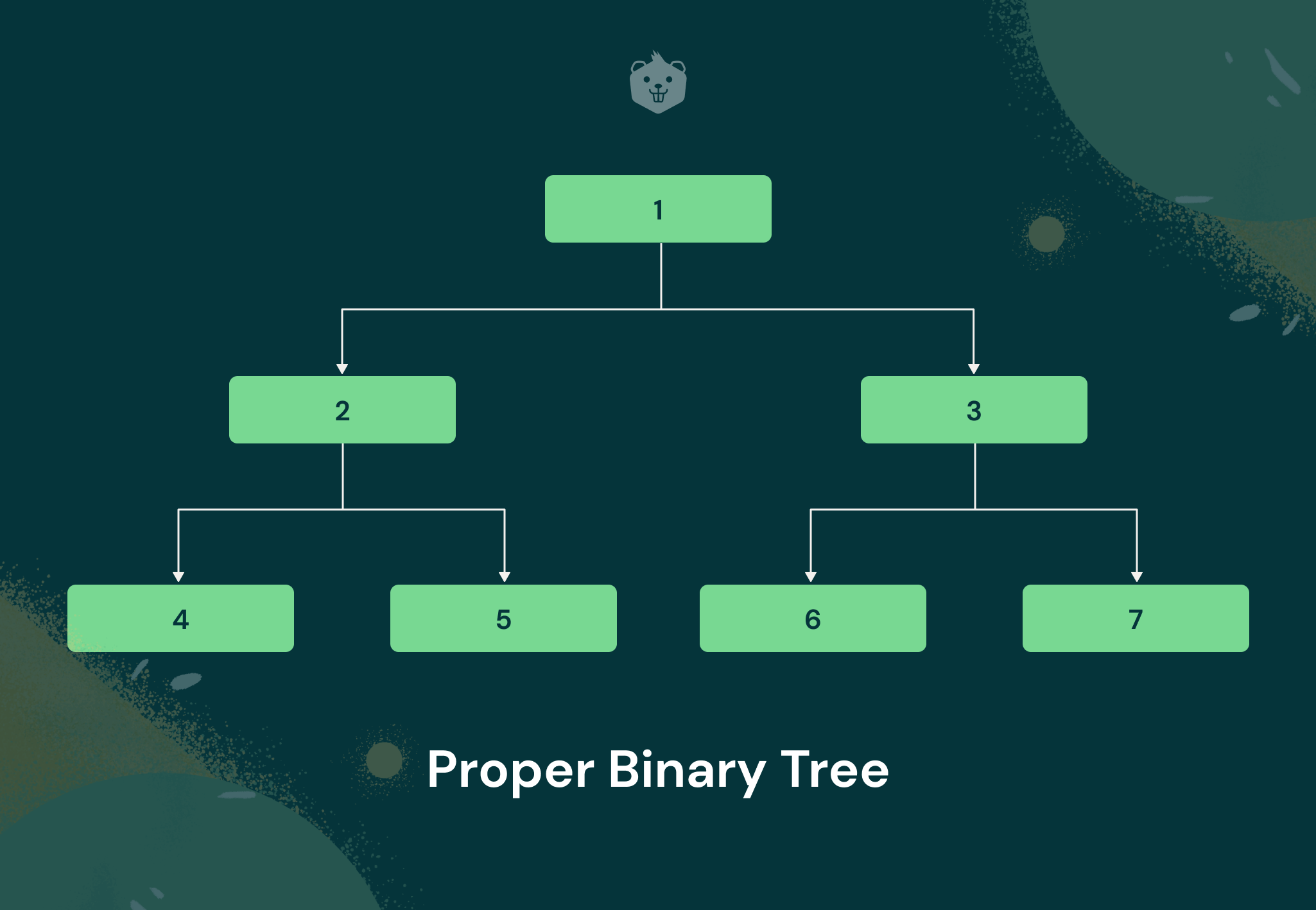
It's clearly observable that every node (except the leaf nodes) has strictly 2 children. That is why it is also known as a strict binary tree.
Complete Binary Tree
It is a type of binary tree data structure in which all internal nodes are completely filled except for the nodes at the last level. In the last level, the nodes must be filled from as left as possible. Given below is an example of a complete binary tree.
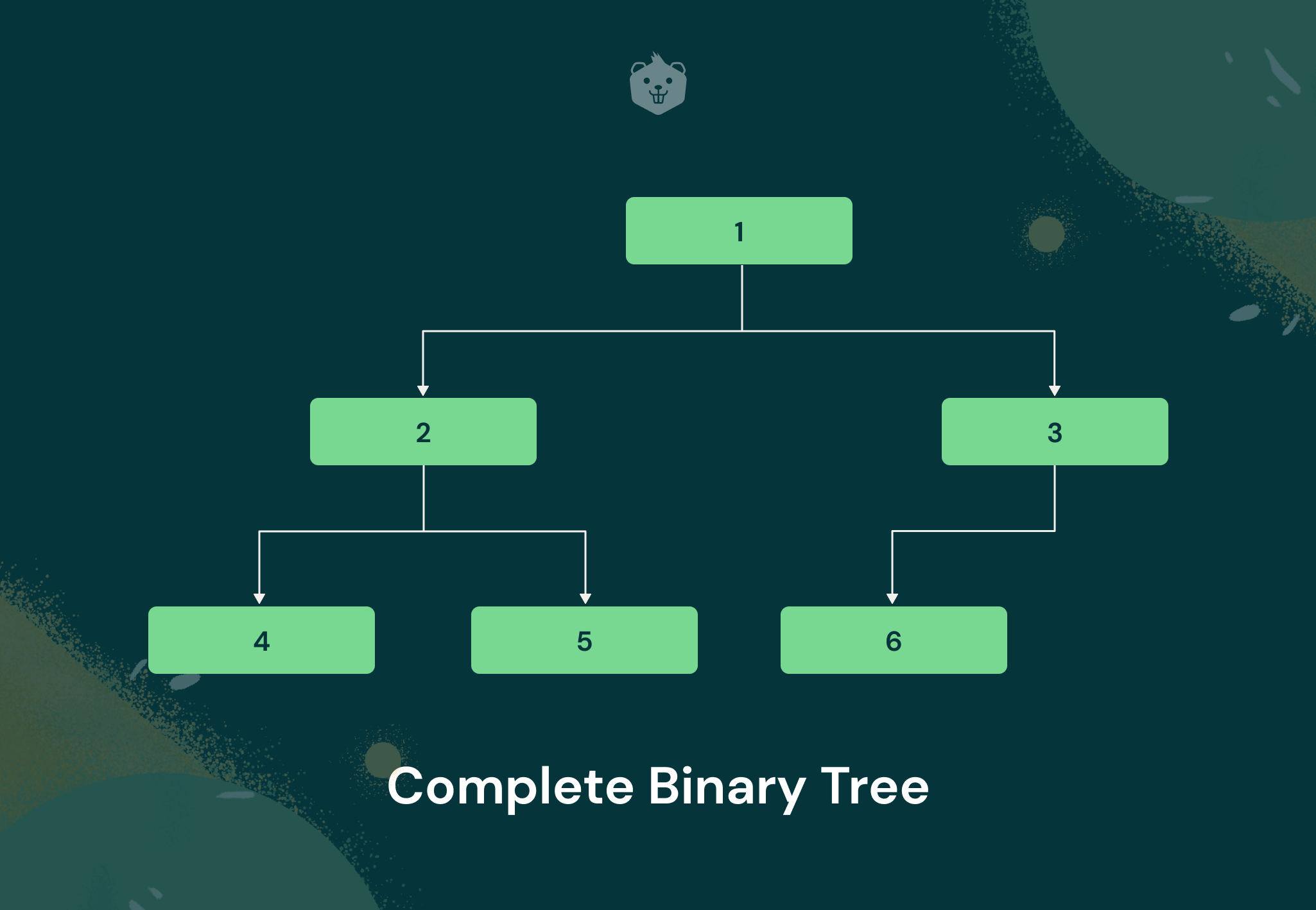
You can clearly observe that the nodes at the last level (marked 2 and 3) are filled from the left and are not necessarily filled.
Properties
- Maximum number of nodes present in a complete binary tree of height h: 2^(h+1)-1.
- Minimum number of nodes present in a complete binary tree of height h: 2^h.
- Minimum height of a complete binary tree: log2(n+1) - 1.
Perfect Binary Tree
A tree is said to be a perfect binary tree if each of its nodes has strictly 2 children and all its leaf nodes are at the same level. Given below is a simple illustration of a perfect binary tree.
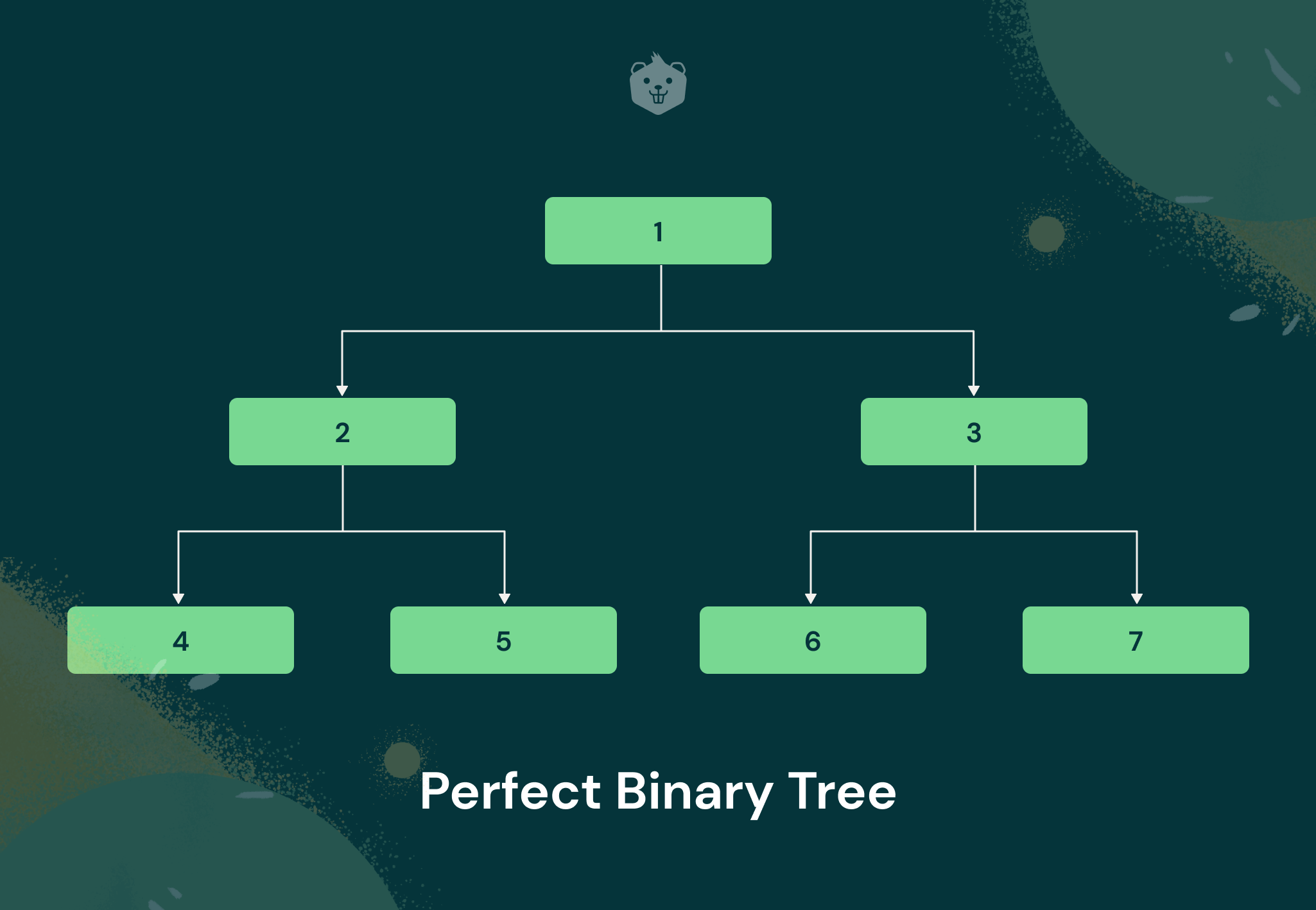
As you see, the leaf nodes are all at the same level and all the internal nodes have exactly 2 children each. This is what categorizes it as a perfect binary tree.
Test your understanding
Given below is another example of a binary tree. Can you guess whether it is a perfect binary tree or not?
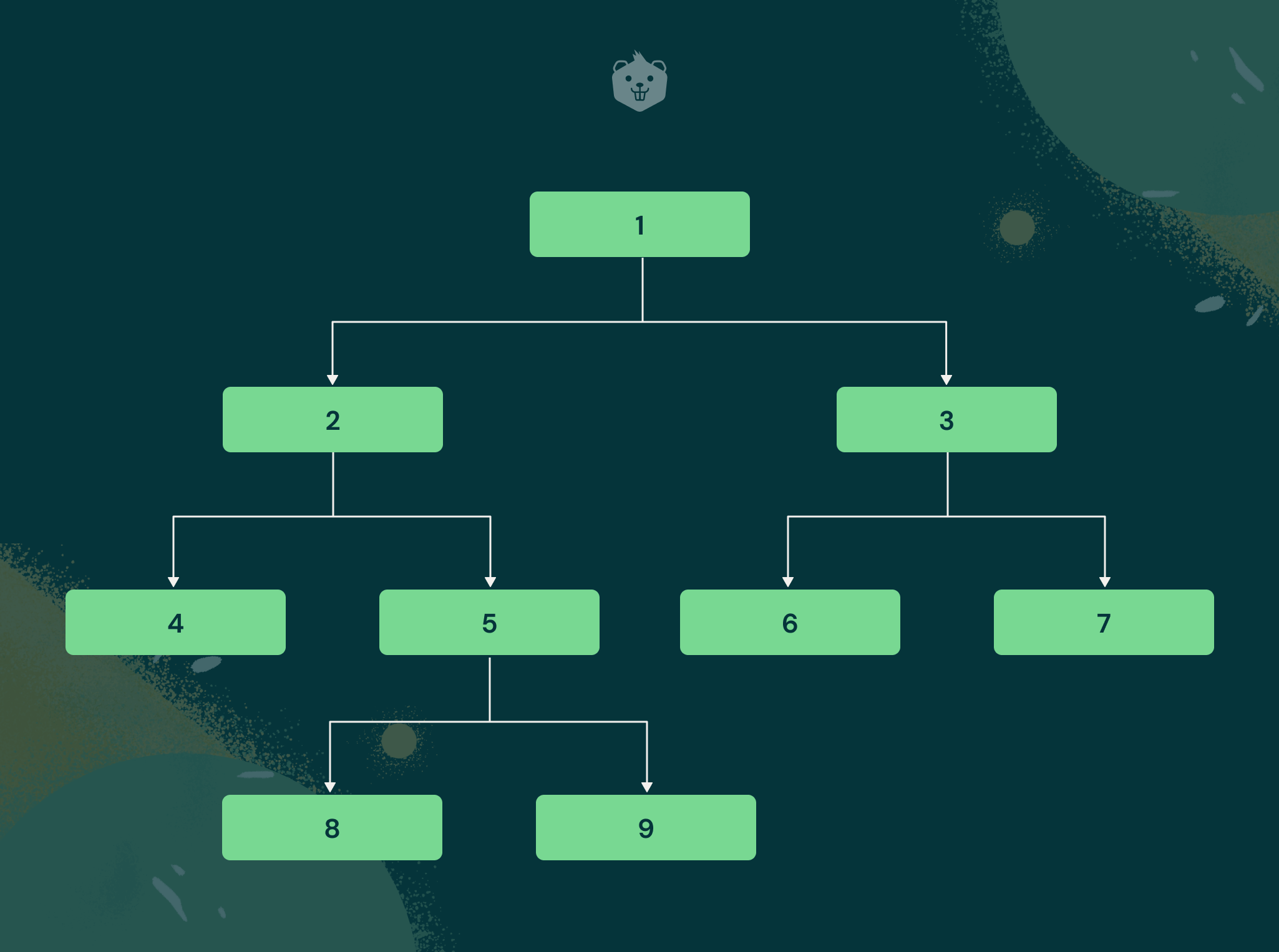
Guess the answer??
.
.
Okay, the answer is a no. It's not a perfect binary tree for the simple reason that although the internal nodes have strictly 2 children each, the leaf nodes are not at the same level. This is an example of a proper binary tree instead.
Degenerate Binary Tree
A binary tree is categorized as a degenerate binary tree if all its internal nodes have strictly one child node each except for the leaf node. Here's a diagram to illustrate this:
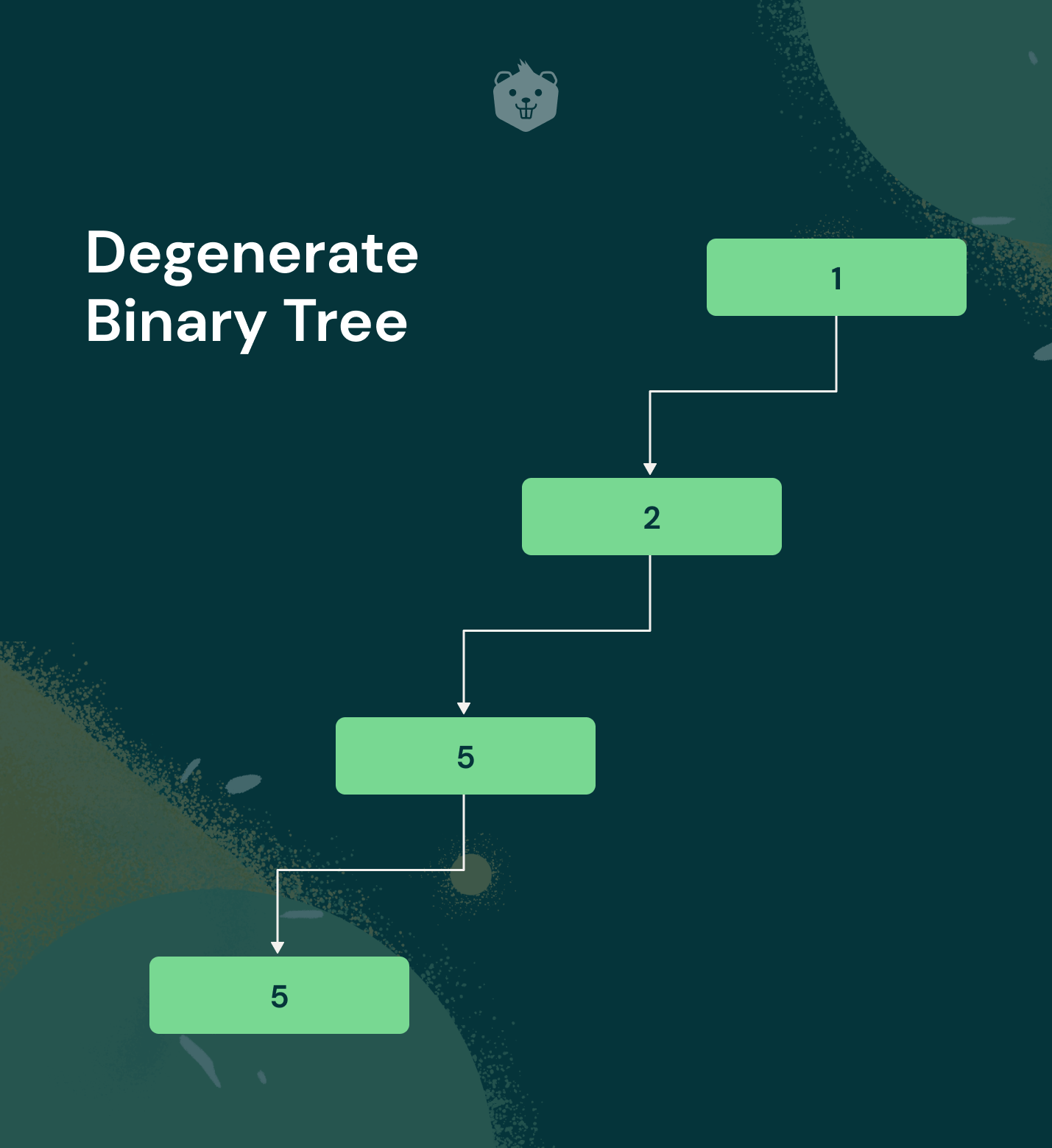
Here's another example to elucidate this concept:

In both the diagrams given above, each of the nodes in the tree has strictly one child node except for the terminating leaf node.
If all the nodes of a degenerate binary tree have a left child node only, it forms a left-skewed binary tree.
Similarly, if all nodes of the tree have a right child node only, it forms a right-skewed binary tree.
Balanced Binary Tree
In a balanced binary tree data structure, the height of the left and right subtrees for each node differ by at most 1. Some common examples of balanced binary trees are AVL trees and Red-Black trees.
Still unclear? Here's an example to understand balanced binary trees better.
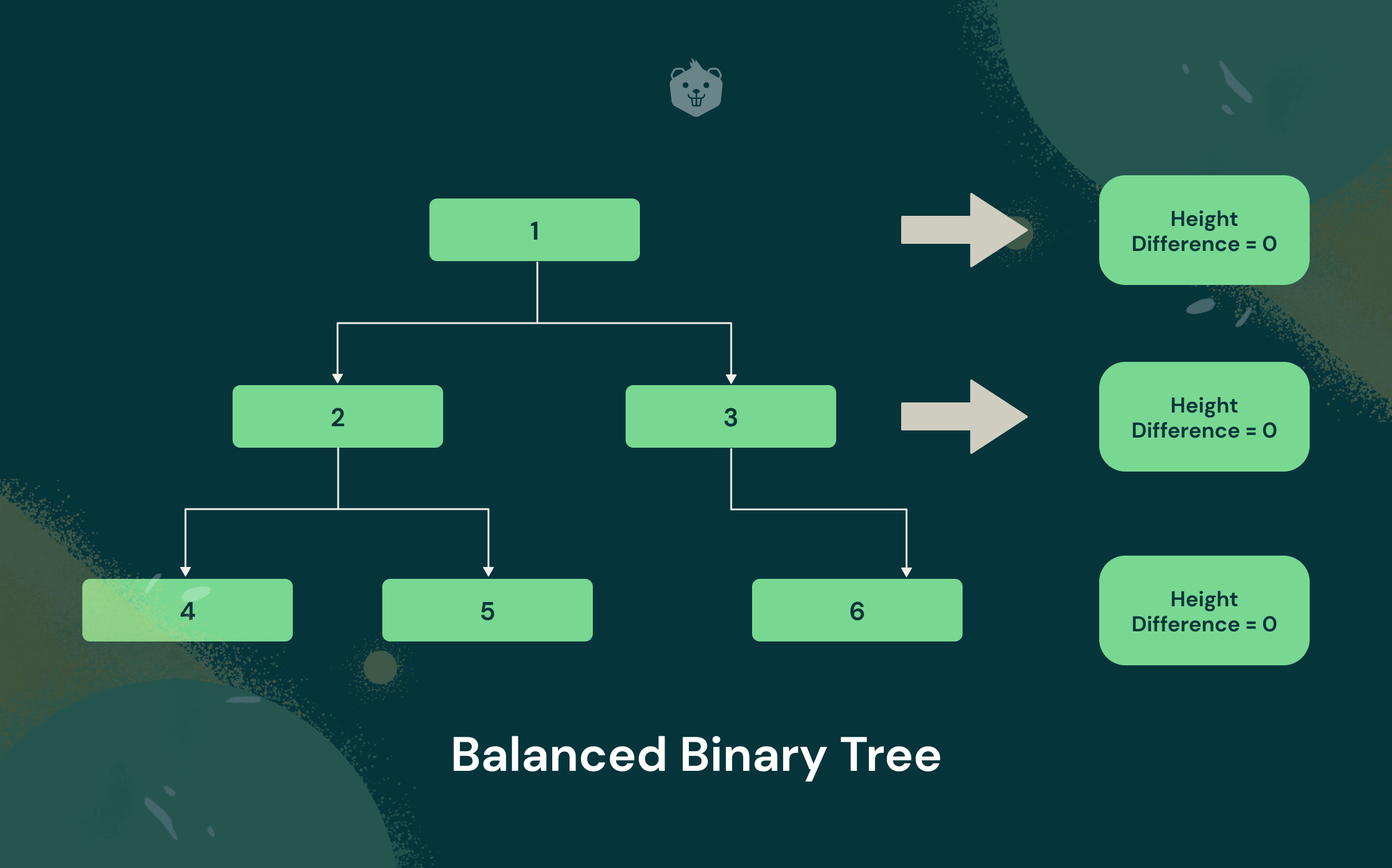
Node 1
- Height of the left subtree for given node = 2
- Height of the right subtree for given node = 2
- Difference = 0
Node 2
- Height of the left subtree for given node = 1
- Height of the right subtree for given node = 1
- Difference = 0
Node 3
- Height of the left subtree for given node = 1
- Height of the right subtree for given node = 1
- Difference = 0
Test your understanding
Given below is another diagram of a binary tree. Can you guess whether it is a balanced binary tree or not?
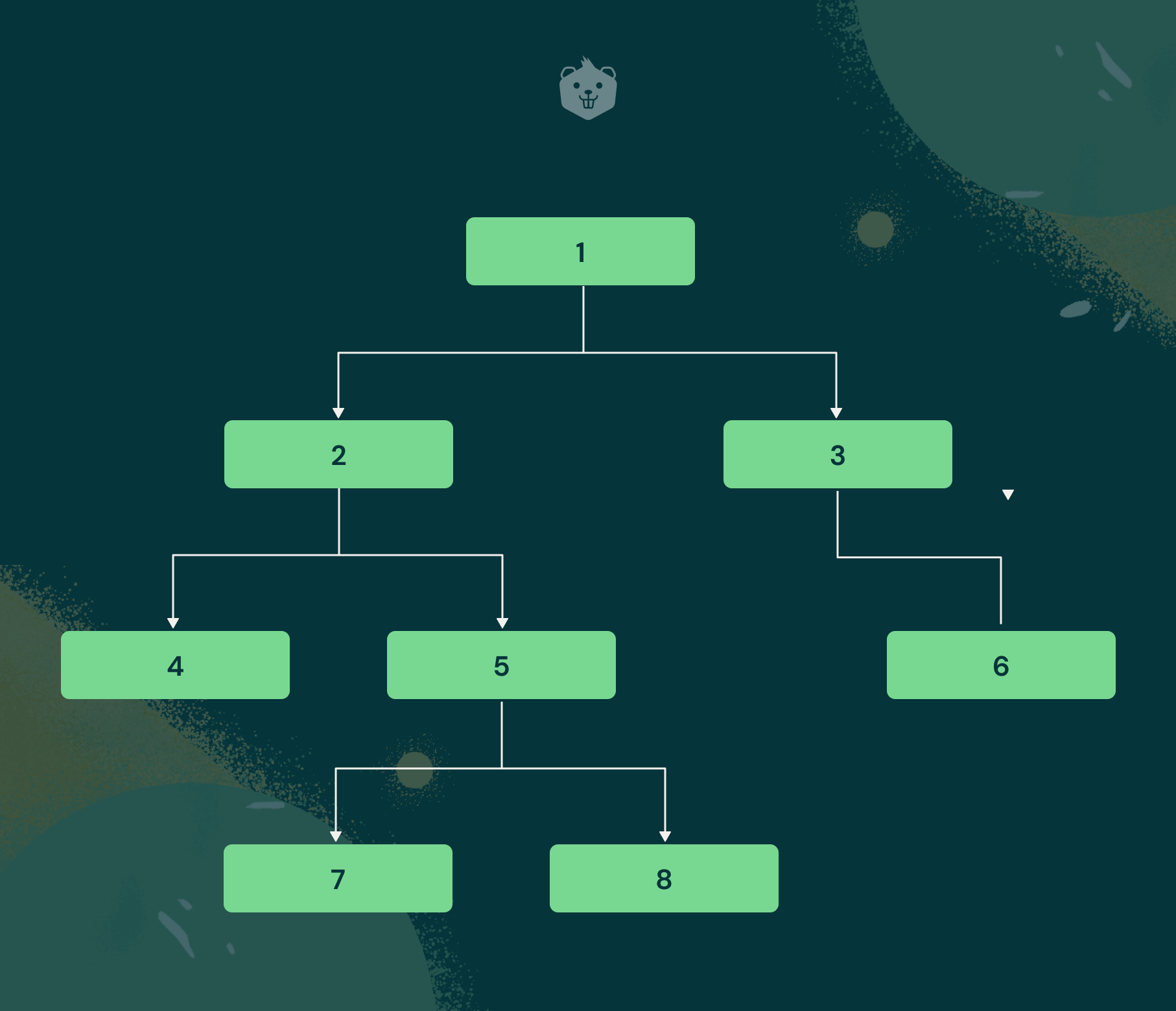
Struggling with the answer?
.
.
The correct answer is yes, it is a balanced binary tree, for the simple reason that the difference of at most 1 still holds for every internal node.
Binary Tree Implementation in C++
Given above is a simple C++ implementation of a binary tree data structure. Once executed, the following tree structure gets stored in memory:
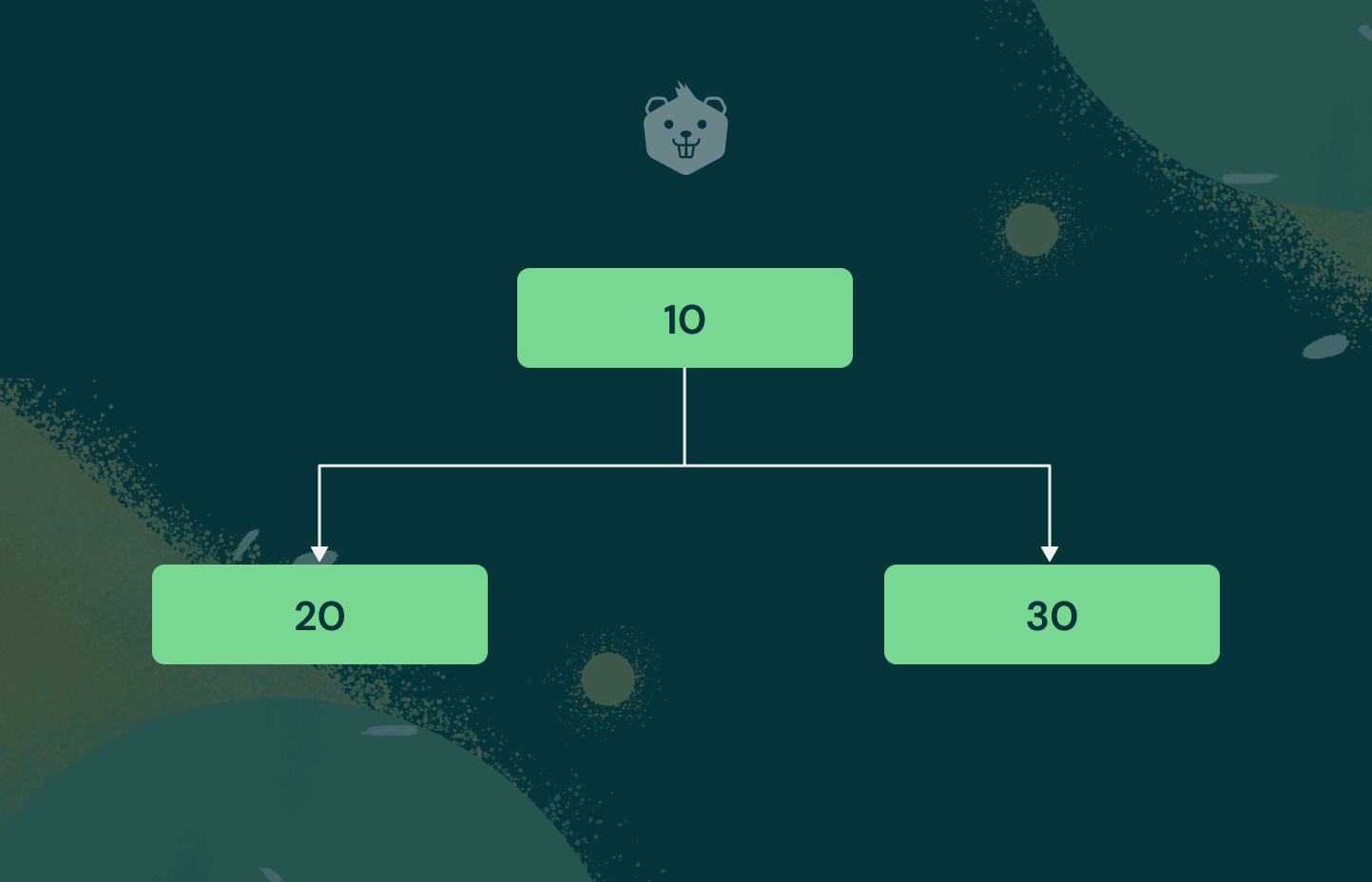
1. First define a struct for the basic outline of your binary tree. Inside the main() function, you can observe that the root node is defined first which is assigned a value of 10.
2. Next, define the left and right children nodes of the root node and assign values of 20 and 30 respectively.
3. This is the basic structure of a binary tree in C++.
4. Of course, you can expand on it to form more complex tree structures but this should be a good foundation to start with.
Real-Life Implementation of Tree Data Structure
- Machine learning employs decision-based algorithms which are heavily reliant on the tree data structure.
- SQL databases use B-Tree for indexing.
- The file directory structure of our laptops or computers resembles a hierarchical tree structure.

Conclusion
Binary trees have a lot of applications in different fields including machine learning, computing systems, databases, computer networking among many others. In other words, its applications are limitless.
Of course, we've barely touched the surface when it comes to the conceptual aspects of binary trees. You can branch out from this article and explore the transversal algorithms associated with trees, how it relates to other data structures in existence, or you may as well crunch out some problems related to them.
Before you go, could you please share this article with your friends or on your social media handles? Also if you enjoyed reading this article, please don't forget to give a thumbs up.
Happy coding!!!